CS 248 - Introduction to Computer Graphics
Autumn Quarter, 2001
Marc Levoy
Lecture notes for Tuesday, October 30 (and part of Thursday, November 1)
I'll finish the taxonomy on Thursday (November 1).

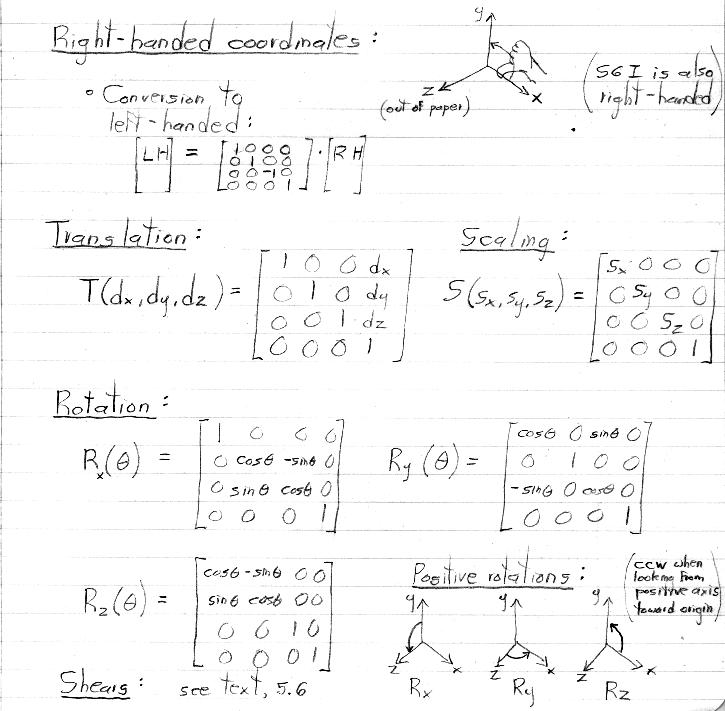
Thus, the 3D Cartesian coordinates occupy the W = 1 three-dimensional subspace
within 4D homogeneous space.





Note that the function f transforms one 2D space to another 2D space. No matter what kind of warp we want to apply to the image (including perspective, as we shall see), we don't need a Z-coordinate. We formalize this notion in the next section for one class of functions - linear transformations in 2D. We implement these transformations by converting 2D Cartesian coordinates to 3D homogeneous coordinates, which we multiply by a 3 x 3 matrix.

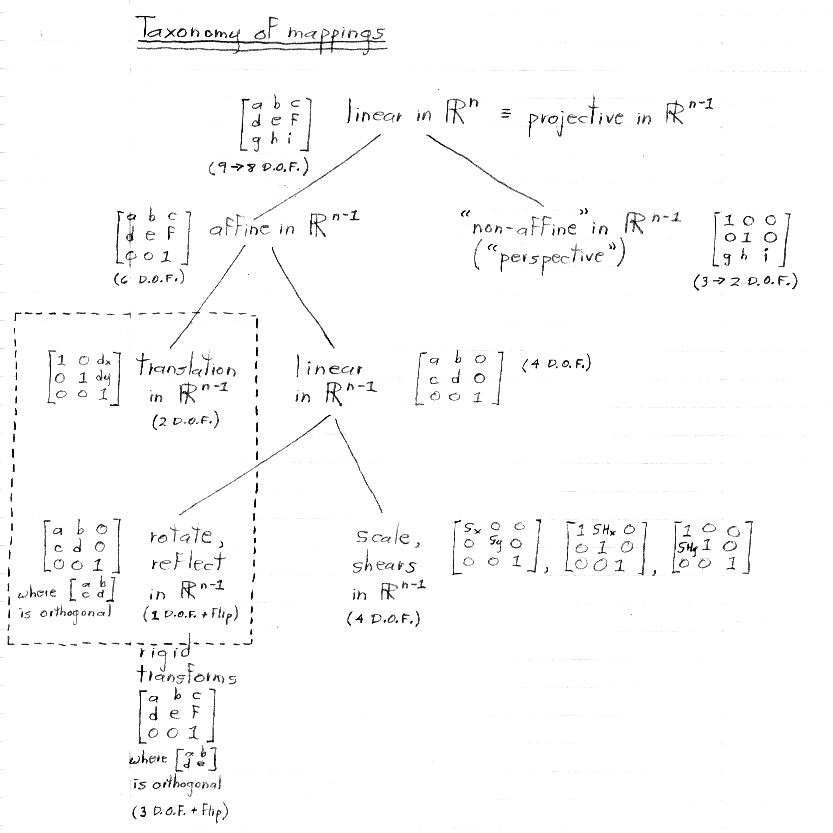
n = 3 in the above taxonomy.

In other words, linear mappings in 2D are those that can be accomplished using a 2 x 2 matrix multiplication with the coordinates (not raised to any power) as inputs.
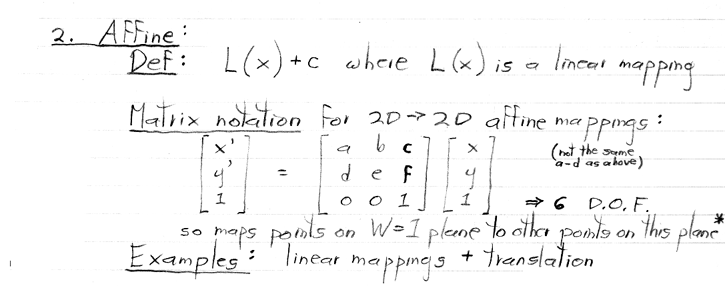
* For this reason, the W = 1 plane is sometimes called the 2D affine space associated with the 3D homogeneous coordinate space.

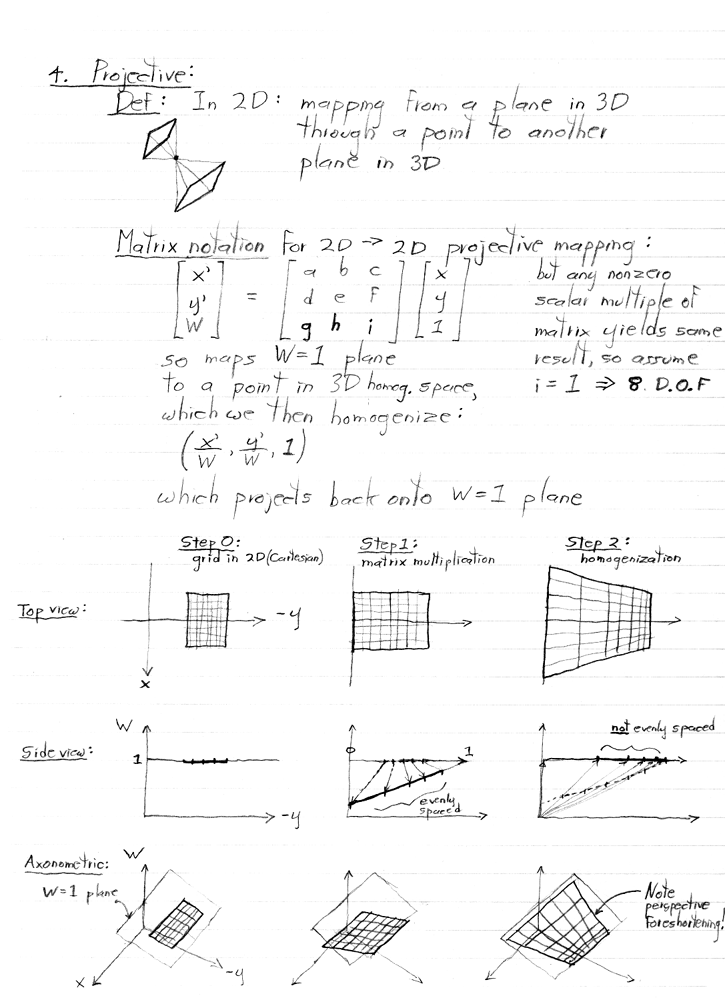
Note also that this perspective foreshortening required a division (by W) to accomplish!
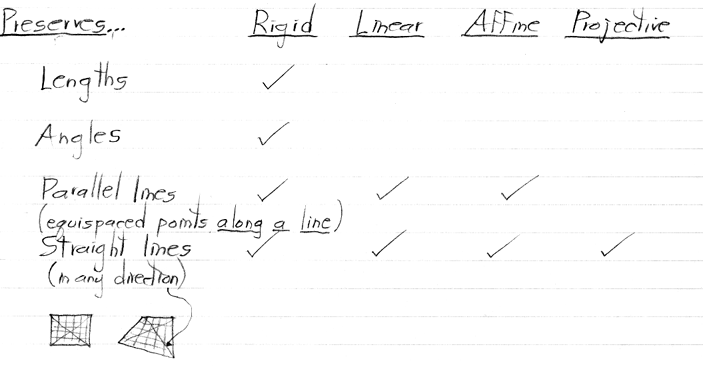
The columns of this chart are assumed to be in the same space. In particular, if we are talking about rigid, affine, and projective transformations in Rn-1 with respect to the taxonomy, then the linear column also refers to linear transformations in Rn-1, not in Rn.