CS 248 - Introduction to Computer Graphics
Autumn Quarter, 2005
Marc Levoy
Lecture notes for Tuesday, October 4
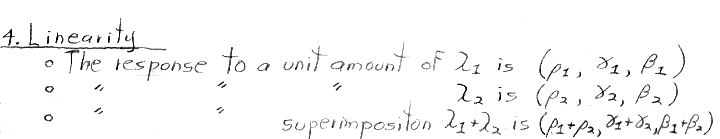

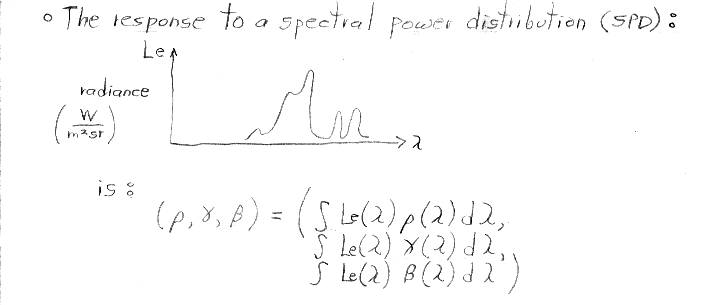
In my notes above, "n lambda sub 1" means "n units (possibly fractional) of radiance of a stimulus having wavelength lambda sub 1. It doesn't mean a unit stimulus of wavelength n x lambda sub 1.


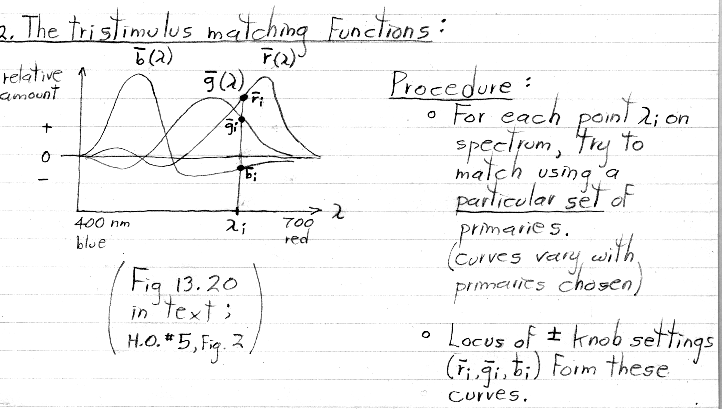
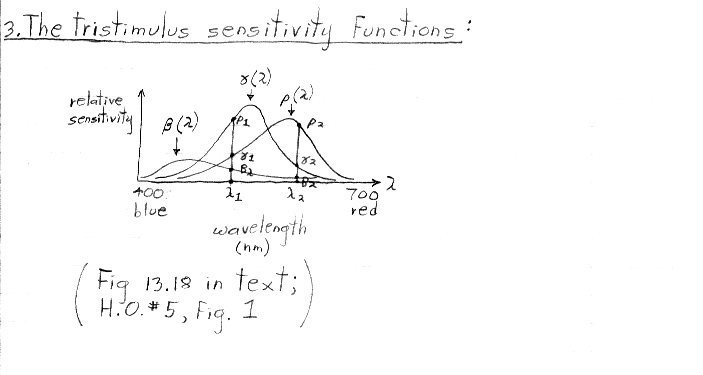
Note: the place in the figure above where the red and blue matching functions cross, and the leftmost crossing of the red and green matching functions, should both be exactly on the zero line, for reasons explained below. Figure 2 in handout #5 is more accurately drawn and places these crossings correctly.
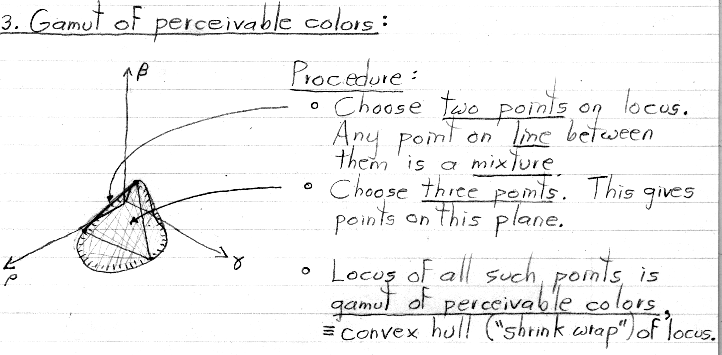
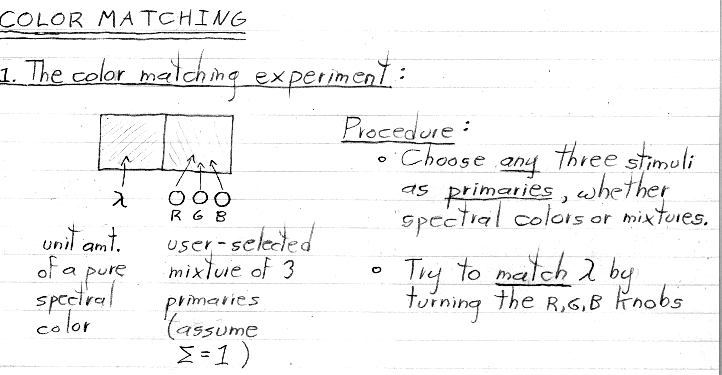
Initially, this is the same situation as depicted in the previous section (#3), except that we make it a point to choose pure spectral colors whose amplitude=1 points lie roughly on the red, green, and blue parts of the spectral locus. We are also allowing mixtures of these R,G,B primaries whose sum lies between zero and one, rather than being normalized to one. This leads to colors that occupy the volume between the shaded plane and the origin. This volume is called the gamut of reproducible colors for these particular primaries.
Note that this gamut touches the locus of spectral colors at only three points (other than the origin), These points correspond to the three primaries. In terms of Thomas Young's matching experiment, the knob for one primary is set to its maximum at each of these points, and the other two knobs are set to zero. Looking at figure 2 of handout #5, these points correspond to the three places on the lambda axis where one plot is high and the other two are at zero. Note that these places correspond to the three wavelengths listed beside the figure.
If the R,G,B primaries are not pure spectral colors (i.e. single wavelengths), then they can be represented as mixtures of pure spectral colors. In this case, their amplitude=1 points will fall somewhere strictly inside the volume shaded above, rather than falling on the spectral locus. The gamut of colors reproducible using these non-pure primaries will shrink accordingly, to span these new points.
Remember also that the primaries don't need to be in the red, green, and blue parts of the spectral locus. Choosing different wavelengths (or mixtures of wavelengths) as primaries will move the amplitude=1 points (and the corresponding gamut) around. However, the gamut will always fall within the convex hull ("shrink-wrap") of the spectral locus, because that represents all the (normalized) responses possible in our visual system, and therefore the full range of colors we humans can see.
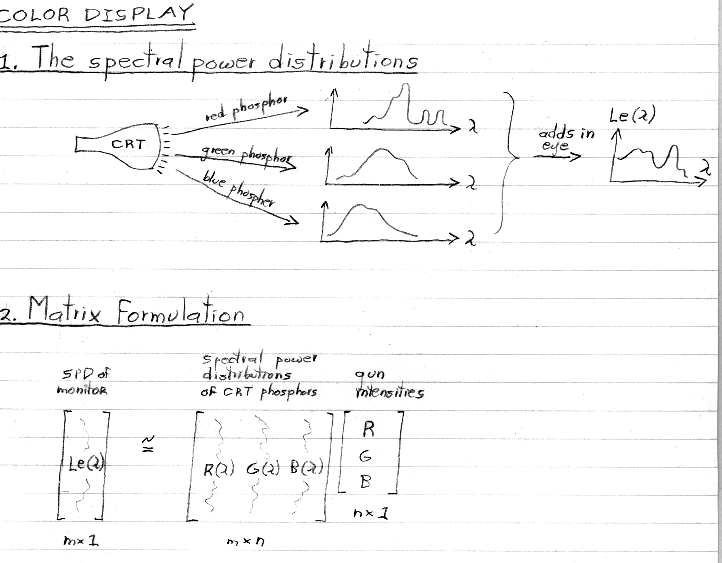
A good example of a system that employs non-spectral R,G,B primaries is a color raster display...

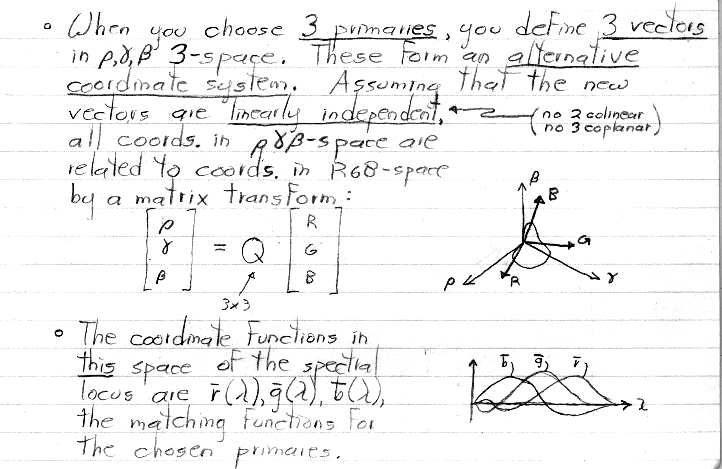
Note: As in the earlier figure, in the plot above, the red and blue matching functions should cross exactly on the zero line.