
CS 248 - Introduction to Computer Graphics
Autumn Quarter, 2008
Marc Levoy
Lecture notes for Thursday, October 9 (second half of class)
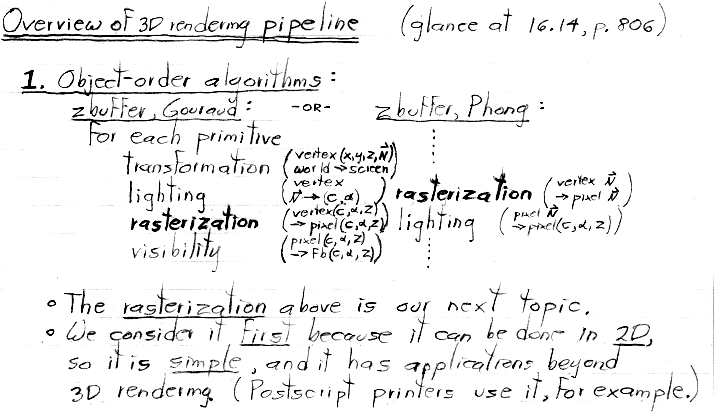


Except for assumptions 1 through 4 immediately below, the following section on
line drawing was skipped in class. It is included here for completeness. You
will not be held responsible for it on exams.






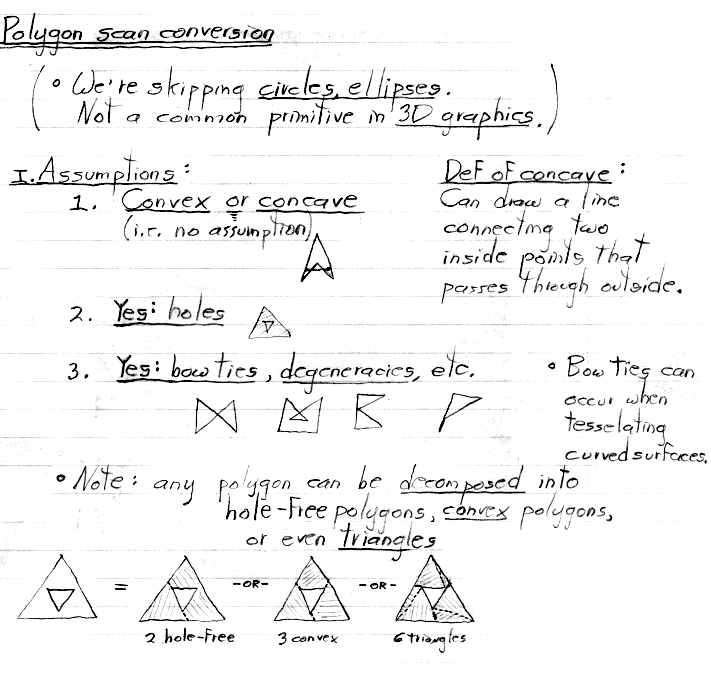
The algorithm that follows, which is taken from section 3.6 in the textbook, handles self-intersecting (e.g. bow-tie) or degenerate polygons naturally, even polygons with holes. As mentioned in handout #7, you will need to handle the first two types in project #2, but not the third. By the way, handling these cases by decomposing them into triangles is not allowed, at least for the project.
Note that steps 3.2 (remove edges) and 3.2.5 (sort the active edge table) should be performed before step 3.3 (fill the scanline), despite the physical order in which they appear in the list above. Re-sorting the active edge table seems to happen frequently, but it typically isn't expensive. In particular, if you have introduced a new edge in step 3.1, then you will need to move it to its correct position in the table. However, this is only done at events, in fact only once per edge of the polygon. Even if you have not introduced an edge, you must look through the table for edges that may be out of order because they have crossed after the x increments of the previous step 3.5; these edges will need to be swapped in the table. This check must be done on every scanline, not just at events, but in the vast majority of cases no swapping will be necessary, so the cost of this check is low. As I mentioned in class, manipulations to the edge tables typically represent a small fraction of the cost of a rasterizer. Most of the time is spent in step 3.3, filling pixels.
By the way, the suggested code for updating the X-coordinate in step 3.5 is an integer-only solution, lifted from Bresenhham's algorithm. If you're willing to use floating-point arithmetic, then the increment becomes just the (floating-point) slope, with no if-test necessary.

In general, a polygon rasterizer should fill only and all sample positions that fall inside polygon edges. In previous versions of project #2, we also required students to rasterize their polygons such that they meshed perfectly, i.e. with no holes or doubly-drawn pixels. To satisfy this requirement, care must be taken when sample positions coincide with polygon edges or vertices, as discussed above. This year, we do not require this. Thus, the only rule you must obey in your project this year is that all sample positions that are strictly inside a primitive, i.e. not coincident with a vertex or edge, should be filled, and all sample positions that are strictly outside a primitive should not be filled. This means that in the sliver polygon above, you should not fill any samples in the second column, immediately above the word "gap". Whether you fill the sample at the leftmost vertex is up to you. After anti-aliasing, assuming you use enough supersamples, the left tip of the polygon should look approximately the same whether you do or not. In particular, it should like like a knife-edge thinner than a pixel. This apparent thinness arises from the pixel under the vertex having a color that is a blend of the polygon's color and the background color.

The algorithm described in section II is very general, and it's useful from a didactic standpoint to see how a general plane-sweep algorithm works, but what do real graphics cards use? The answer is proprietary, and it may vary among manufacturers, but at the least they always decompose polygons into triangles. Shown above is one algorithm for fast rasterization of triangles. A different algorithm is: "Triangle scan conversion using 2d homogeneous coordinates", by Marc Olano and Trey Greer, in Proc. ACM SIGGRAPH/Eurographics Workshop on Graphics Hardware, 1997. Since I didn't cover these algorithms in class, I'm not holding you responsible for them.