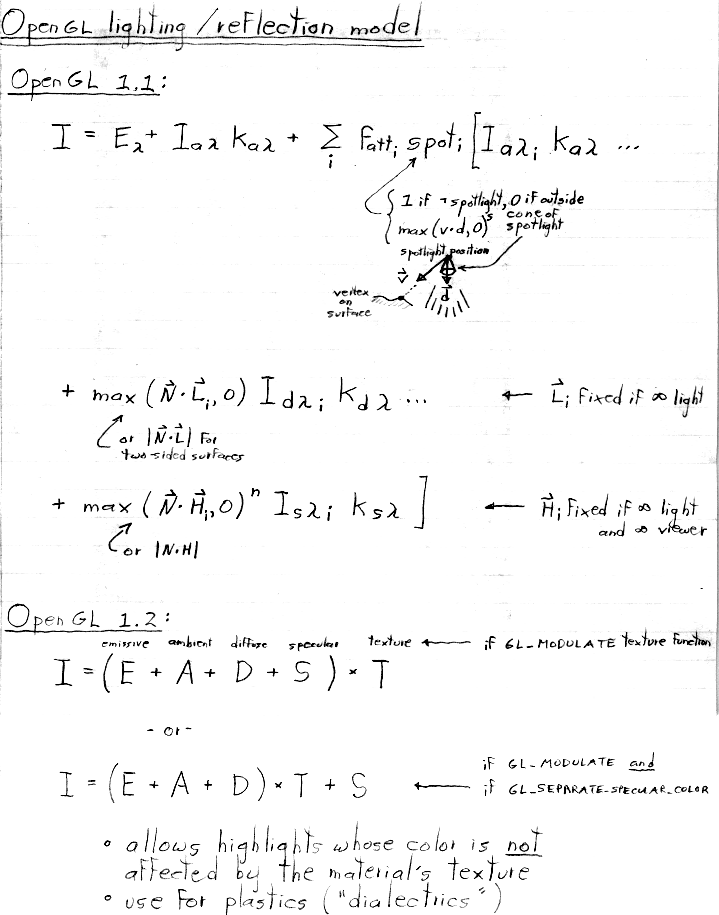
CS 248 - Introduction to Computer Graphics
Autumn Quarter, 2008
Marc Levoy
Lecture notes for Thursday, November 20
Press here for the Powerpoint slides about measuring BRDFs.

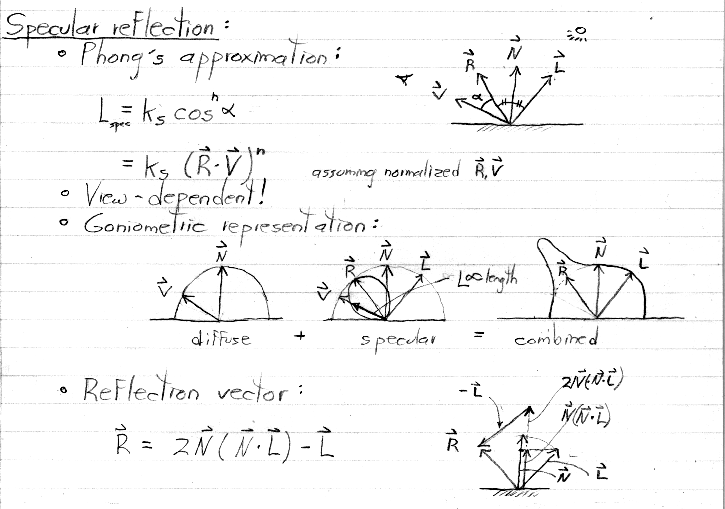

To save time, I did not cover the issue of local versus infinite L and V in class. I'm leaving it in the notes in case you're interested. Infinite L, i.e. infinitely distant lighting, is invoked in OpenGL by setting the homogeneous coordinate W = 0.0 when specifying the position of the light source in (for example) glLightFv(x,y,z,W). Infinite V, i.e. infinitely distant viewing, is invoked in OpenGL by setting GL_LIGHT_MODEL_LOCAL_VIEWER = GL_FALSE in glLightModeli(). Note that moving the viewer to infinity in this way is only for the purpose of lighting, not viewing, i.e. it changes the intensities computed for surfaces, but it does not change the geometry of the image you see.
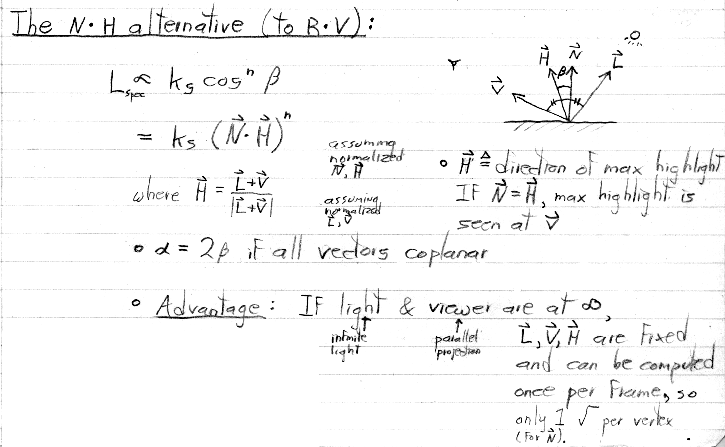

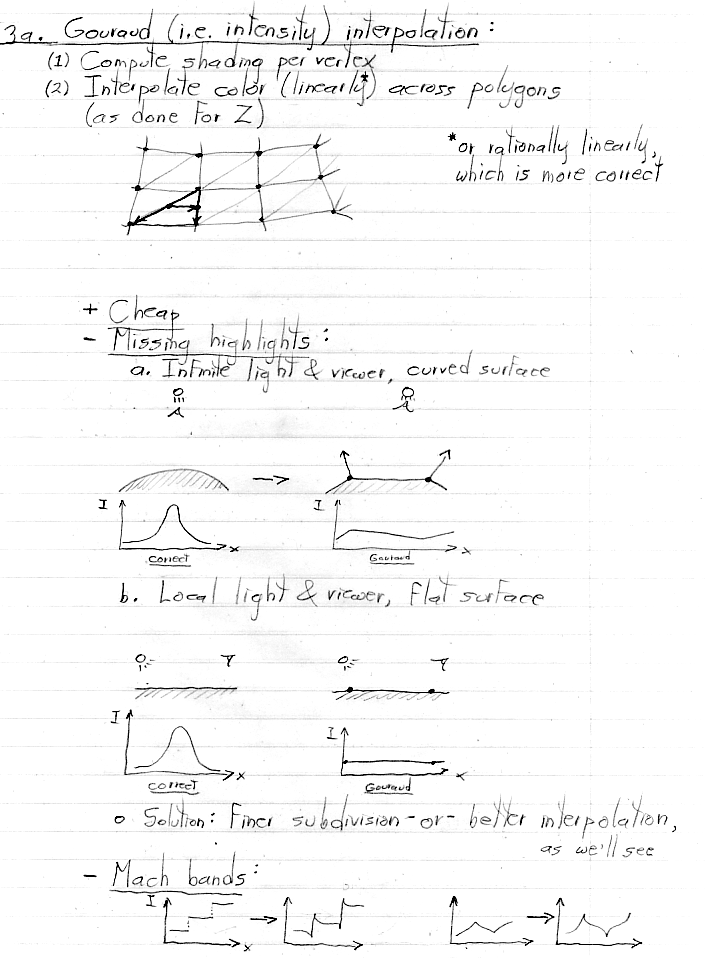
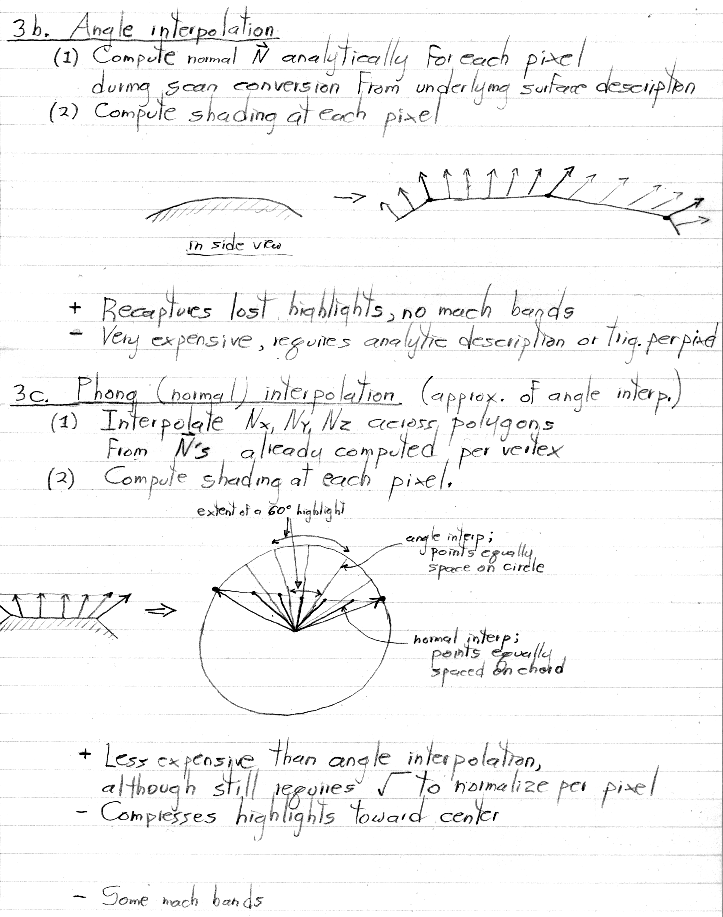
OpenGL natively supports only Gouraud (i.e. intensity) interpolation. Phong (i.e. normal vector) interpolation is not supported natively, but it can be implemented (during rasterization) using the flexible shading architecture available in most modern hardware accelerators. Angle interpolation would be harder to implement. However, assuming modest changes in normal vector direction from vertex to vertex, the visual difference between normal and angle interpolation is small. OpenGL does not specify whether Gouraud interpolation should be linear or rational linear. Modern graphics boards implement it using rational linear interpolation.
I skipped polygon mesh shading in class today so that I could cover the OpenGL lighting/reflection model in time to be helpful on your video games. I will cover this material in class on December 2.