CS 248 - Introduction to Computer Graphics
Autumn Quarter, 2008
Marc Levoy
Lecture notes for Tuesday, October 21

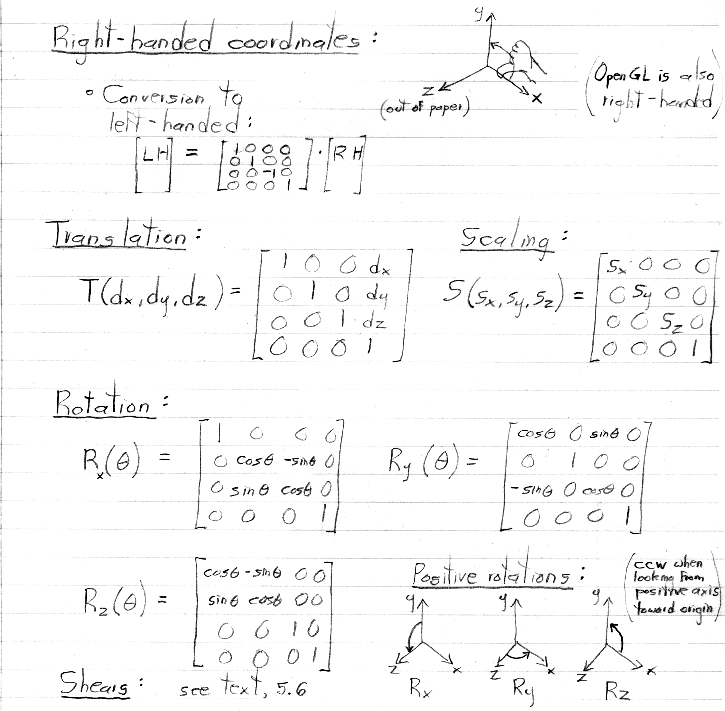
Thus, the 3D Cartesian coordinates occupy the W = 1 three-dimensional subspace
within 4D homogeneous space.

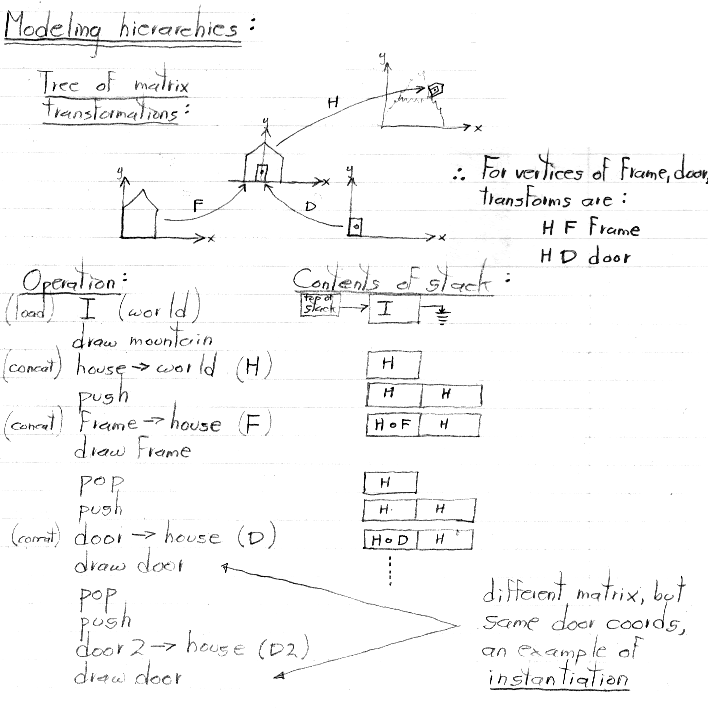
Concatenating a matrix (let's say F) with the matrix at the top of the stack (let's say H), denoted "H circle F" above and said "H composed with F", means perform the matrix multiplication H times F (in that order). We sometimes describe this multiplication by saying that F is right-concatenated onto H. Remember that matrix multiplication is not commutative, so the order does matter.





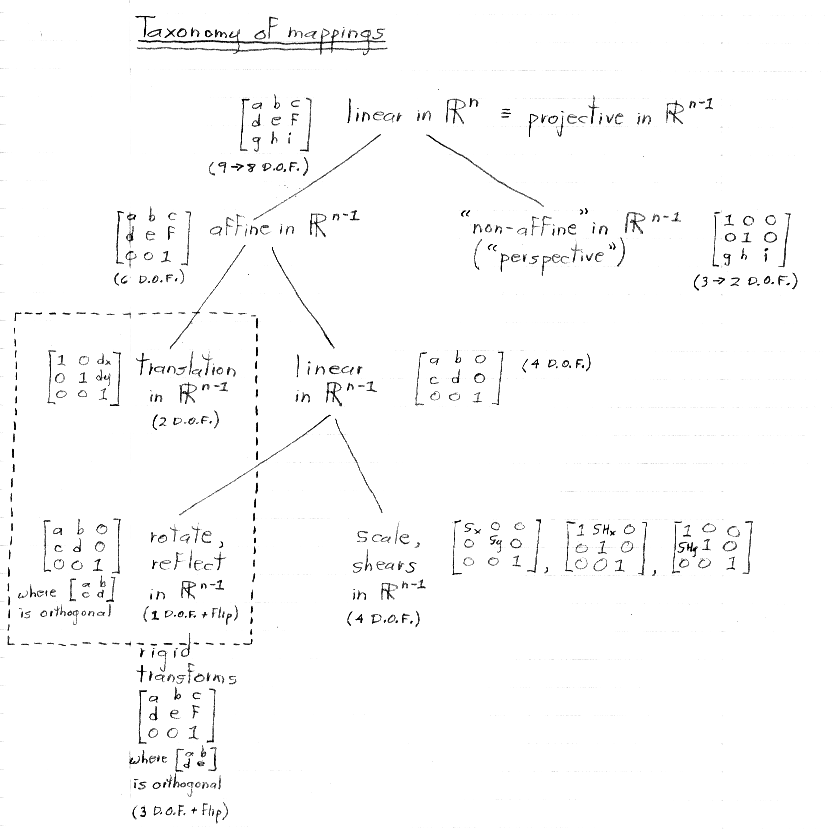
n = 3 in the above taxonomy.

In other words, linear mappings in 2D are those that can be accomplished using a 2 x 2 matrix multiplication with the coordinates (not raised to any power) as inputs.
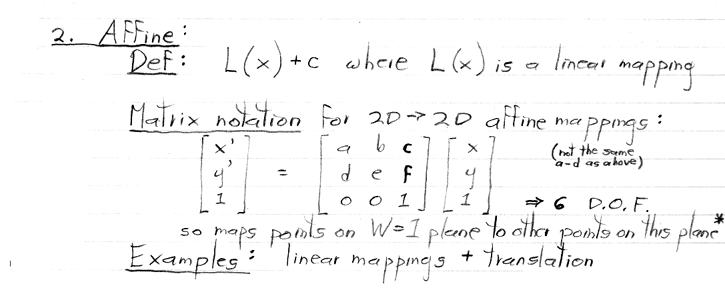
* For this reason, the W = 1 plane is sometimes called the 2D affine space associated with the 3D homogeneous coordinate space.

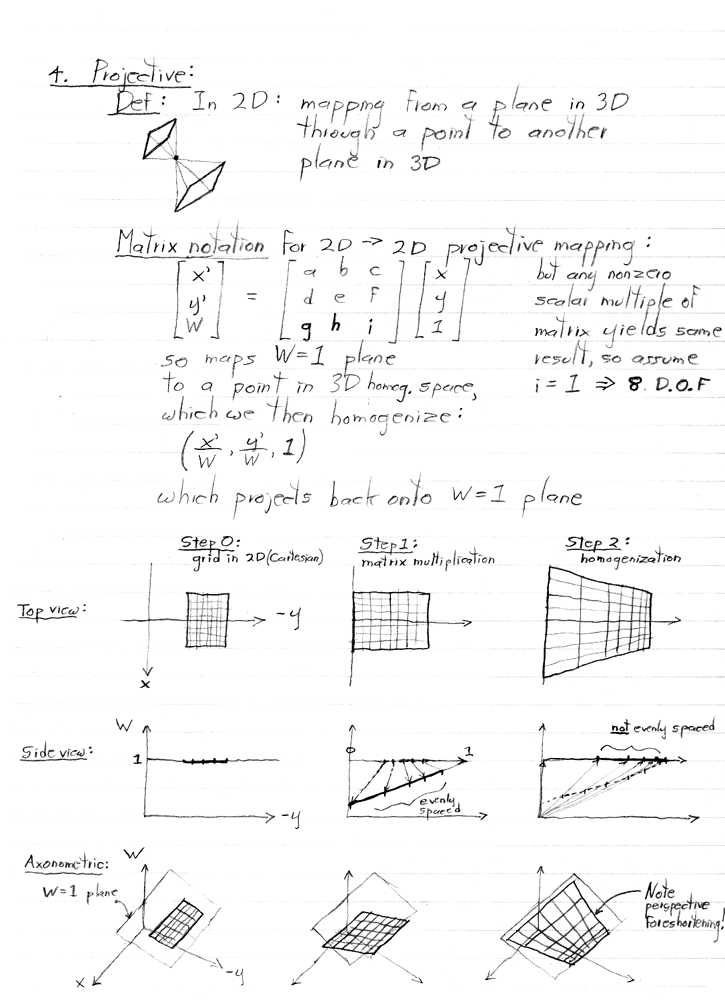
Note also that this perspective foreshortening required a division (by W) to accomplish!
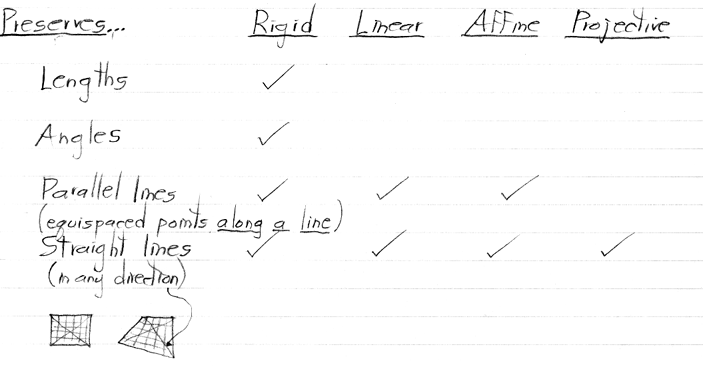
The columns of this chart are assumed to be in the same space. In particular, if we are talking about rigid, affine, and projective transformations in Rn-1 with respect to the taxonomy, then the linear column also refers to linear transformations in Rn-1, not in Rn.