CS 248: Introduction to Computer Graphics

Pat Hanrahan

Handout

Overview

MOAN is documented extensively on the class WWW pages. Its input is a text file describing a scene tree, which represents a modeling hierarchy. The figure below shows a simple scene tree describing a sphere squeezed between two cylinders. Rendering takes place by traversing the tree (an inorder walk), each node performing some GL calls specific to its type when visited:

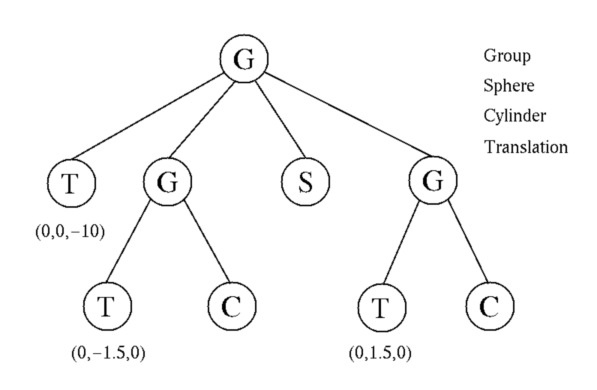
A scene tree for a sphere squeezed between two cylinders. The light node required to make the objects visible (see the text) is omitted here for clarity.

• A group node pushes the current modelview matrix - using glPushMatrix() - before traversing its children, and pops it immediately after all its children have been traversed - using glPopMatrix().
• A transformation node, be it a translation, rotation, or a scale, post-multiplies the current modelview matrix by a translation, rotation, or a scale matrix respectively - using glTranslate*(), glRotate*(), or glScale*(). The entries of this matrix are stored in the node, and, for joint transformation nodes, they can be interactively modified using MOAN.
• A primitive node renders an object - using glBegin(), glEnd(), and glVertex*(). For example, a sphere primitive node renders a polygonal approximation to a sphere of unit radius centered at the origin, while a cylinder primitive node renders a polygonal approximation to an uncapped cylinder of unit radius wrapped around the y axis and extending from y=-0.5 to y=0.5.

/usr/class/cs248/assignments/assignment3/examples/simple.sc

MOAN also supports animation via keyframing. That is, you may manually associate different values for each parameter of a joint transformation with different frames, called keyframes; MOAN interpolates these parameter values at in-between frames, and can thus play back a smooth animation.

Finally, MOAN supports lighting. That is, scene tree nodes can create lights and affect the appearance of subsequent primitives - using glLight*() and glMaterial*(). You need not worry about lighting for this assignment, except for one detail: make sure your scenes define at least one light, so that your objects are not lost in the dark; to this end, create a single light node near the root of your scene by copying a light definition from an example scene file.

Before you try to use MOAN, you should review all class material relating to hierarchical modeling and animation:

1. Chapter 3 of the OpenGL Programming Guide.
2. Lectures 11 and 12 of the Course Notes.
3. Lectures 11, 12, 13, and 16 (especially the BBOP video).
4. Chapters 5 through 7 of Computer Graphics: Principles and Practice.

The philosophy of MOAN: MOAN is a simplified relative of SoftImage and Open Inventor, two commercial modeling and animation systems. In the past, this assignment required students to write actual OpenGL code. MOAN shields you from coding details and encourages trial-and-error experimentation by eliminating the need to recompile every time you change your model. MOAN is too simple and crude at times, as it is designed to match very closely OpenGL's approach to modeling; still, it's a good stepping stone to commercial systems. To complete the assignment, you need not look at MOAN's source code (except for the interpolation routines which are fully encapsulated); however, as the source code is very simple and extensively documented, you are welcome to peruse it and see how simple it is to code up the very powerful abstraction of hierarchical modeling.

Warning: MOAN is a brand new product, designed and coded by your TA Toli. As such, it may still have bugs. So

• it may be upgraded as the due date nears; notifications on major bugs will be mailed to the class-wide mailing list, while minor tweaks will be announced via the class WWW pages only;
• if MOAN ever crashes or exhibits incorrect behavior, please call Toli anytime at (415) 723-0618 and let him know; for medical reasons, please don't use e-mail.

Modeling an Articulated Figure (20 points)

1. (10 points) have a depth of at least 5, containing at least 20 transformation nodes (either static or joint transformations), at least 5 of each type (scale, translation, rotation),
2. (5 points) contain at least 20 primitives, and
3. (5 points) represent a realistic object. Given the limited capabilities of MOAN, we do not expect you to produce Jurassic Park dinosaurs; a caricature, a stick figure, a 5 year old's drawing turned 3D, or anything bearing the semblance of a real object is adequate.

Hints:

• Images of example scene trees are available on the class WWW pages.
• When the raptors are slow, an easy way to get MOAN to maintain an interactive pace is to render your primitives as wireframes. If this does not suffice, you may compose your model solely of line primitives; but note that, although it is acceptable to turn in such a stick figure, it may be hard to animate (see the next part of the assignment).
• Draw your scene tree on paper as in the above figure before generating any scene files. A picture is worth 1,000 words and 10,000 files, where messy text can hide the underlying hierarchical structure.
• Primitive nodes render objects of a predetermined, fixed size. Use scale transformations to elongate, or otherwise change the proportions of your primitives.
• Use comments profusely to delineate distinct sections of your hierarchy. To re-indent messy scene files, you may load your file in MOAN, save it from MOAN, and read it back into your editor. The drawback of this approach is that the new file will not retain the comments in the input file.
• You only need to use group, primitive, and static transformation nodes for this part of the assignment. But since in the next part you'll be substituting joint transformation nodes for some static ones, you might want to plan ahead. Also, MOAN allows you to interactively edit the parameters of joint transformations, and thus allows for limited interactive modeling.

Animation (40 points)

1. (20 points) your scene tree should contain at least 10 animated joint transformation nodes, at least 5 translations and 5 rotations, each with at least 7 keyframes,
2. (10 points) the figure should have the same configuration in the first and last frames of the animation (that's what makes it a cyclical motion),
3. (5 points) the animation should be smooth, with adequate keyframes to prevent sudden jumps, and
4. (5 points) the animation should depict a plausible, familiar movement, in a realistic fashion. As we mentioned earlier, we do not expect you to reproduce Species monsters moving in caves; however, we want something more than the "mating ritual of Magellan penguins dancing in anti-gravity fields," consisting of European - no offense intended; the writer is European, too - avant-garde artists in black, violently jerking their limbs all over the place.

Hints:

• To turn a static transformation into a joint, set the first and last keyframes of the joint to the same value as the static transformation.
• Keyframe numbers are real quantities between 0.0 (first keyframe) and 1.0 (last keyframe) in the scene files; however, MOAN displays the current frame as an integer from 0 to 300.
• MOAN allows you to interactively edit the parameters of joint transformations at keyframes; thus, it allows for limited interactive keyframing.

Multiple Figures (10 points)

Multiple Views (20 points)

1. the adjoint A of the matrix on the top of the modelview stack is calculated,
2. A post-multiplies a regular viewing matrix whose entries are determined by the camera node - this matrix is generated using glOrtho() or gluPerspective(), depending on the camera type -,
3. the result becomes the new viewing transformation, and
4. the traversal is pruned (aborted).

Hint: figure out by hand what effect is achieved by traversing camera nodes in the fashion stated above. Trial-and-error experimentation using MOAN may be helpful, but concentrated thinking while taking a shower will achieve better results. Browsing through section 8 of lecture 9 in the Course Notes, as well as section 4 of lecture 15, might help...

Interpolation (10 points)

1. (2 points) modifies no keyframes by accident,
2. (2 points) does not miss any in-between frames,
3. (2 points) interpolates all keyframes,
4. (3 points) makes the derivative of the interpolated parameter tend to zero as the animation approaches any keyframe, and
5. (1 point) is not excessively slow. You will only lose this point is your code is really inefficient, e.g. due to multiple passes over the in-between frames.

Hint: understand the code of our linear interpolator before starting to write the Hermite one.

Extra Credit

For more extra credit, build a scene consisting of 12,000 figures riding unicycles on a Hilbert curve. (Just kidding.) Good luck using the raptors for that.

Conclusion: Turning in Your Work.

If any of your files fail to parse, your grade for the corresponding parts of the assignment will be reduced by 50%.