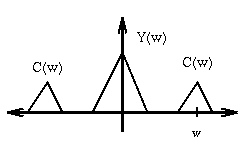
C(x) and Y(x) in the Fourier domain
This is a plot of the maginitude of the combined spectrum
4. The following questions concern signal processing and its application to computer graphics.
4A. (10 points) Define the following three terms, and dicuss how they are related.
Suppose two functions Y(x) and C(x) are combined with the following
procedure:
1. The function C(x) is multiplied by sin(wx) (where w=2(pi)f is called the
carrier.)
2. And then added to the signal Y(x).
What is the interpretation of this operation in the frequency domain? (Hint: this is most easily shown with a figure in frequency space; for simplicity assume that the spectra for C and Y are humps centered at the origin of frequency space.)

How might the functions C(x) and Y(x) be extracted from the combined signal?
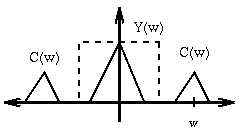 First, let's assume that C(x) and Y(x)
are bandlimited - i.e. they don't contain frequencies larger than w/2 or
smaller than -w/2 in this case. To extract Y(x), multiply Y(w) by a box
function of width w centered at the origin. Apply the inverse Fourier
transform to get the result.
First, let's assume that C(x) and Y(x)
are bandlimited - i.e. they don't contain frequencies larger than w/2 or
smaller than -w/2 in this case. To extract Y(x), multiply Y(w) by a box
function of width w centered at the origin. Apply the inverse Fourier
transform to get the result.
To extract C(x), either apply a high pass filter to eliminate Y, or apply a
low-pass filter (i.e. a box) that has been shifted to w. This will yeild a
copy of C(w) centered at w. Convolve this with FT(sin(wx)). This
yeilds a copy of C(w) at the origin, a copy at C(w), and a copy at C(2w).
Multiply this by a box centered at the origin and do an inverse Fourier
transform to recover C(x).
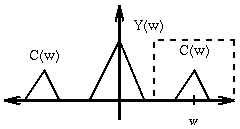 Multiplying by a shifted box to get one copy of C(w) centered at w
Multiplying by a shifted box to get one copy of C(w) centered at w
|
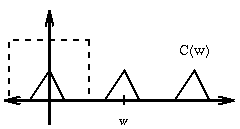 Convolving with FT(sin(wx)) and multiplying by a box to get a copy of C(w) at the origin. |
Suppose the function Y(x) is the luminance of an image, and the function C(x) is the color (don't worry about what color space). What happens to the extracted function C(x), if Y(x) contains frequencies greater than 1/2 the carrier frequency? How would this appear to the observer?
First, let's assume that we always use a box of width w for a reconstruction filter (so it extends from -w/2 to w/2 if centered at the origin). This is reasonable since we don't know in advance the bandwidth of either C or Y, so we just choose to use the same reconstruction filter for both signals. Thus, if Y(x) contains frequencies greater than w/2, then Y(w) will extend past w/2, and thus not all of it will be captured by the reconstruction filter for Y. Worse, some of the spectra of Y will now be in C's reconstruction filter, and so high Y frequencies will masquerade as C frequencies. The result: high frequency changes in luminance will have distorted color. The best example of this is looking at someone wearing a shirt with thin stripes on a television. The stripes will appear colored because of the artifact described here.
Some special notes: